A sequence whose elements are calculated from earlier elements in the series is a linear recurrence. The Fibonacci sequence (0, 1, 1, 2, 3, 5, …) is an example:

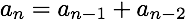
With the equation and the first two numbers in the sequence, you can calculate the rest.

There are more complicated sequences that are also linear recurrences:

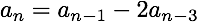
You can multiply each term by a constant and still have a linear equation. Here the coefficients are 1, 0 and -2.

You can also multiply terms by things that aren't constant:

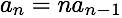
This is called a nonhomogeneous linear recurrence equation. The previous examples were homogeneous linear recurrence equations.

Calculating one of these sequences can obviously be pretty tedious, so let's do it with Python.

def recurrentSequence(fn, k, sequence):
""" A generator for linear recurrence equations

fn: a function to calculat a_n from sequence
k: how many terms fn uses to calculate a_n
sequence: The first k elements of the sequence
"""

# n indexes the sequence
n = k

while True:
    try:
        Sn = fn(sequence, n)
    except IndexError:
        # if fn requires more terms than we have that's bad
        print('fn needs more terms than were provided')
        break

    sequence.append(Sn)
    sequence = sequence[-k:]

    yield Sn

    n += 1

Given a function, the number of terms are in the function, and the first elements of the sequence the generator calculates the subsequent elements. This is an example of a generator. Precomputing an infinite sequence isn't very practical, instead recurrentSequence() generates elements as they're requested. recurrentSequence() saves the elements it calculates so that they don't have to be recalculated when in order to get the next element in the sequence, but it only saves the k elements needed to calculate the next element.

Here's a Fibonacci example:

In [1]: def fib(s, n):
            return s[0]+s[1]

In [2]: g = recurrentSequence(fib, 2, [1,1])

In [3]: g.next()
Out[3]: 2

In [4]: g.next()
Out[4]: 3

In [5]: g.next()
Out[5]: 5

And an example of a nonhomogeneous equation:

In [6]: def lines(seq, n):
             return seq[0]+n

In [7]: g = recurrentSequence(lines, 1, [1])

In [8]: g.next()
Out[8]: 2

In [9]: g.next()
Out[9]: 4

In [10]: g.next()
Out[10]: 7

In [11]: g.next()
Out[11]: 11

Fork it on GitHub